URGENT UPDATE: New research from Ankara University reveals groundbreaking insights into the complex world of pseudo-evolute curves and caustic surfaces, crucial in the field of differential geometry. This study, conducted by mathematicians Hande Nur DALKILIÇ and Yusuf YAYLI, addresses significant gaps in understanding how to generate specific caustic developable surfaces by manipulating light sources and base curves.
The findings, published today, offer a fresh perspective on three types of caustic developable surfaces: rectifying, osculating, and normal. These insights could have profound implications for various applications in mathematics and physics, particularly in fields utilizing optics and geometry.
In their study titled “Pseudo-evolute curves and caustic surfaces,” DALKILIÇ and YAYLI examine how light interacts with developable surfaces—shapes that can be created by bending a flat sheet without stretching it. By adjusting the direction of light sources reflected off mirror surfaces, they demonstrate how to derive specific caustic surfaces, enhancing our understanding of these mathematical constructs.
Key Findings: The researchers clarify essential concepts, including the Frenet frame and Darboux frame, which are pivotal in analyzing space curves and surface-borne curves. They provide detailed definitions for various forms of curvature—critical for understanding the behavior of these surfaces under different light conditions.
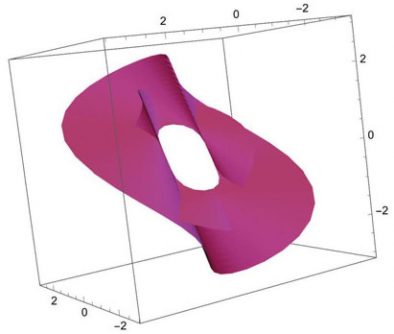
1. **Rectifying Caustic Surfaces**: The study reveals that when a light source is positioned in the negative unit binormal direction of a unit-speed space curve, the resulting caustic forms a rectifying developable surface. The striction curve in this scenario corresponds to the pseudo-evolute curve of the base curve.
2. **Osculating Caustic Surfaces**: When observing a unit-speed surface-borne curve, the research indicates that positioning the light source in the negative auxiliary vector direction yields an osculating caustic developable surface. This surface also aligns with the flat approximation of the base surface.
3. **Normal Caustic Surfaces**: The findings further confirm that aligning the reflected vector with the unit normal direction of the base curve results in a normal caustic developable surface, which reflects the normal approximation characteristics of the base surface.
The validation process of their findings is equally compelling. The researchers verify that when the geodesic curvature of the base curve is zero, the striction curve of the osculating caustic aligns with the pseudo-evolute of the space curve. Similarly, for normal curvature, the normal caustic’s striction curve matches.
Incorporating practical examples, such as helicoids, the study provides calculations and visualizations that bolster their conclusions, making the complex subject matter accessible and engaging.
As this research is now available for full open access, it has the potential to inspire further exploration in the fields of mathematics and physics. The implications of these findings extend beyond theoretical mathematics, offering fresh insights that could influence optical engineering and related disciplines.
For those interested in diving deeper into this vital research, the full text is accessible at: https://doi.org/10.1631/FITEE.2400930.
Stay tuned for more updates on this developing story as it shapes the future of differential geometry and its applications.